Chasing the elusive convective
dynamic in bicycle pelotons
In our paper, Collective behavior and the identification of phases in bicycle pelotons [1] we used data from two mass-start velodrome races to demonstrate the presence of two main phases of peloton dynamics: 1) a stretched phase, and 2) a compact phase exhibiting features of synchronized cyclist motion and more disordered collective motion.
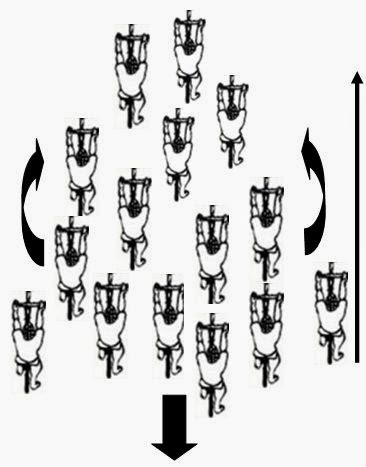
We did not, however, clearly show what I have in past described as a "convective" phase, illustrated below in Figure 1 (from [1, 2]) and in Video 1*. Video 1* below contains a short clip of the sort of behavior I am hoping to quantify (not including the solo rider at the end). This phase behavior involves cyclists advancing up group peripheries as cyclists in central regions move effectively backward. This is analogous to a convection dynamic as "hot" riders advance, and "cooling" riders fall back. Although we did not demonstrate the effect in our paper, this does not mean the dynamic did not occur, but it was not sufficiently obvious in the data as derived from two small pelotons of 12 and 14 riders, in two short races both of less than 15 minutes each.
Video 1. Clip of peloton convective motion*
Figure 1. Illustrating the convective dynamic. Cyclists advance up peripheries (curved arrows), while riders in central region drift effectively backward (short thick arrow). Long arrow indicates direction of motion.
In his paper [3], Erick Ratamero demonstrated a Netlogo agent-based model that simulated this convective effect in bicycle pelotons. From the perspective of clearly showing the collective vector pattern formation, Ratamero's simulation is extremely helpful. However, empirical data that clearly demonstrates this effect has still not been documented. The collective pattern formation of the cyclists in Video 1, for example, will have a sinusoidal appearance, which we know by tracking the trajectories of the simulated cyclists in Ratamero's model, as shown in Figure 2.
Figure 2. Sinusoidal pattern of simulated peloton of 100 cyclists in convective motion, applying method in [1] to quantify collective motion, and using Ratamero's MOPED peloton model [3]. Y-axis shows relative positions of each cyclist to all cyclists in the group. X-axis is time.
Recently, I have purchased the rights to video footage of a stage of the Volta au Algarve, a professional bicycle stage race in Portugal. The footage is due to arrive any day now, and I am told it contains 1 hour of continuous overhead helicopter footage. I am optimistic the footage will show long-duration periods of the sort of behavior in Video 1 and that it will be sufficient to clearly establish the convective effect by applying the method of showing positional change as set out in [1].
It is my objective also to demonstrate that this effect occurs in many multi-agent systems, including flocks, herds, and schools, and other biological collectives.
It seems that in order to establish that the principles underlying this effect are indeed self-organizing and naturally occurring (i.e. not an artifact of top-down human design, or simply a result of cyclists' racing strategy), it would be useful to demonstrate that the effect occurs in analogous systems which involve zero motivational influence; i.e. human motivations. Ideally, however, in order to isolate the pure physical principles that underlie the convective dynamic, we would go so far as to exclude even other animal systems in which individuals may also have strategic biases or motivations, and to seek analogous non-biological systems, if they exist or could be established by experimental design.
Such a non-biological system would involve purely physical forces, including a drafting effect that couples the system of particles or agents, a force to drive the collective in uni-directional motion, and some force that allows particles/agents from behind to move in a trajectory that allows for the hypothesized continuous convective motion. Barring a non-biological system like this, we may like to find analogous collective behavior among biological collectives that have minimal or no faculty to make volitional decisions, and whose motions are governed by very simple mechanisms, like bacteria or sperm, for example.
Recently, I came upon this paper by Fortes, A., Joseph, D., and Lundgren, T. Nonlinear mechanics of fluidization of beds of spherical particles (1987) [4]. The authors describe experiments they did that demonstrate interesting two-dimensional dynamics of spheres in water. The authors used the apparatus shown below, which I have snipped and pasted directly from their published paper.
Figure 3. Image from the Fortes paper [4] of the apparatus they used.
Figure 4. Image from the Fortes paper [4], which reads "Figure 5. Drafting, kissing, and tumbling in the vertical two-dimensional bed. The mechanisms are not affected by the inclination of the bed. Re=650."
The Fortes results are very promising from my perspective, and I may be able to demonstrate the analogous convective effect by using a non-biological system similar to the Fortes system. Of course, I would still like to see if the effect occurs in bacteria and sperm and other similar systems, as this does not seem to have been documented. Nonetheless, if we have a drafting effect among falling spheres in water, we have two of the main force considerations that I think are necessary to demonstrate a convective effect: forward motion (here, induced by gravity), and an attractive force by drafting.
My hypothesis is that a small modification to the Fortes et al. apparatus may allow for a set of spheres to tumble two-dimensionally in a convective fashion. The modification I want to try is to curve the apparatus bed laterally. This curve will need to be sufficient to allow spheres to tumble past others and be forced to the peripheries of the group, and then to fall inward toward the bottom of the curve. It seems likely the effect, if it occurs at all, will only occur at the appropriate threshold apparatus angle and bed curvature. The angle and bed curve will dictate the collective sphere velocity, their corresponding drag reduction by drafting, and their relative acceleration at the front of the group toward the bottom of the curve. The reduction in drag due to drafting will, it seems, have to be sufficient to offset the loss of velocity in moving up the curve laterally, while the acceleration down the curve toward the front of the group will have to be greater than the velocity of those spheres rolling down the middle at the bottom of the curve.
This bed curvature replicates a natural inclination for cyclists at the head of a group to gravitate toward a laterally central position (assuming no cross-wind). To show this position, in Figure 1 note the rider at the very top of the image - this rider would be in the "lateral center" of the race course. It is not uncommon for more than one such "lateral center" to occur, each being offset from the center obviously, but well away from the edges of the course.
I suspect that riders tend to gravitate toward this laterally centralized position at the head of the peloton because the lateral center represents physically the safest region between the lateral boundaries of the course; allows maximal peripheral view; multiple options for a line in which to drop backwards if so chosen; maximal options to adjust motion in response to passing movement from behind; and represents the most efficient position ahead of any curves in the road ahead. It will also be interesting to observe how this occurs in other flocking systems, as one suspects this formation is a universal self-organized one.
I have prepared a preliminary version of such an apparatus bed as discussed, shown in Figures 5a and 5b. The lateral curvature is shown in the left-hand image (albeit only in small degree) and the spheres at the bottom of the apparatus are shown in the right-hand image. However, the curvature needs to be modified and other modifications to the apparatus are required to make experimentation more efficient.
Figures 5a and 5b. The proto apparatus for replicating the convective effect in a system of falling spheres in a viscous fluid. Figure 5a shows my attempt at forcing the bed to curve laterally. Figure 5b shows the spheres at the bottom of the apparatus in a laundry soap fluid.
Since the apparatus requires modifications, I cannot of course report any results at this stage. Perhaps it will be entirely a bust, I do not know at this time. However, I have been much inspired by the Fortes paper. In addition to this, I will be looking forward to analyzing the footage from the Volta au Algarve race, although that may take me all summer to do.
References and notes
[1] Trenchard, H., Richardson, A., Ratamero, E., M. Perc. 2014 Collective behavior and the identification of phases in bicycle pelotons, Physica A, Vol 405, 1 July 2014, 92–103
[2] Trenchard, H. 2013. Peloton phase oscillations. Chaos, Solitons & Fractals,Vol 56, November 2013, Pages 194–201
*Home video-cam recording of a live broadcast on http:\\mypremium.tv; Eurosport T.V. I am not certain what race it is from. I have not obtained the rights to use this video.
[3] Martins Ratamero, Erick. 2013. MOPED: an agent-based model for peloton dynamics in competitive cycling. In: International Congress on Sports Science Research and Technology Support, 2013, Vilamoura, icSPORTS 2013, 2013.
[4] Fortes, A., Joseph, D., Lundgren, T. 1987. Nonlinear mechanics of fluidization of beds of spherical particles J. Fluid Mechanics, vol 177, p 467-483